


There may be 50 ways to leave your lover but there are 199 ways to draw a 1000-point star!
As this will take some time to discuss, I'll simply start by providing a link to a computer program which you may use to determine the number of ways to draw a p-point star.
First off, I'd like to applaud you for stepping up to the plate and swinging at this one. Your answer is incorrect as I'm sure you suspected it might be. Since 8-point and 10-point stars can be drawn in only 1 way, there is a chance there's only 1 way to draw a 1000-point star. Your idea to try and come up with a general formula for the number of stars you can draw as a function of the number of points in the star was a very good idea. There's an error in your calculations (w = -1 + 4 or -3) but even the correct value of 3 will show that your formula does not work for 7. Also, just because 8 and 10 are even etc. etc., the conclusion that 1000 might inherit their star counts is a real long shot!
As I attacked this problem I was amazed by the star counts. They are quite erratic. My intuition was that the number of ways you could draw a star would go up as the number of points went up. They do increase, but not "strictly," going down and up along the way.
How a problem is posed is important. As I studied your answer I began to be convinced that you were missing important information. All I did was provide you with the images of the 5-point star, the two 7-point stars etc. I did not tell you the method that was used to construct these stars.
The construction rule for the way to draw the 5-point star goes like this: Start at point A and draw a line to point C. Then draw a line from C to E. Then from E to B. Then from B to D. Then from D back to A.
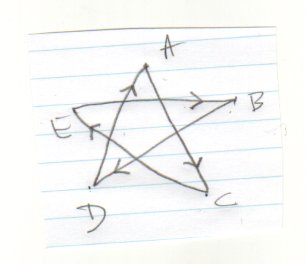
One way to describe this method would be to say "skip 1 letter" each time. If we label the points with numbers we see that the following sequence describes the drawing route.
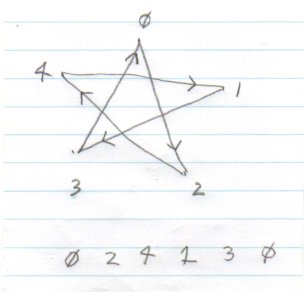
If you try "skip 2" you will see that what you get is not really different but is just the first star, drawn backwards.
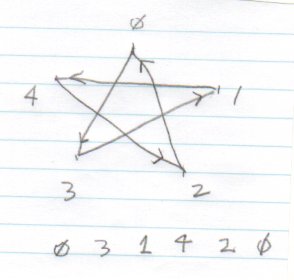
If you try "skip 3" or "skip 4" you get what I call "degenerate" cases.
Try this approach on a 7-point star. Then on an 8-point star. Be very careful when you draw and record your findings
The generated number sequences that contain the number p-1, where p is the number of points, correspond to successfully drawn stars.
Once I realized this fact, I wrote a computer program to do the work for me. You quickly realize you need to do this after trying to draw the stars with 10 or more points!
The program ended up being somewhat tricky to write. I won't bore you with the details but I will point you at the source code.
A "verbose" version of the program shows the sequences generated. Here's what you get when you generate the 4 unique 11-point stars.
STARV - lrb - 1/16/2008 number of points (7 or more) in the star ? 11 want verbose reporting? type 1 for yes, 0 for no ? 1 Let the stargazing begin ... skip 1 : 0 2 4 6 8 10 1 3 5 7 9 0 * skip 2 : 0 3 6 9 1 4 7 10 2 5 8 0 * skip 3 : 0 4 8 1 5 9 2 6 10 3 7 0 * skip 4 : 0 5 10 4 9 3 8 2 7 1 6 0 *Here's what you get when you generate the 5 unique 13-point stars.
STARV - lrb - 1/16/2008 number of points (7 or more) in the star ? 13 want verbose reporting? type 1 for yes, 0 for no ? 1 Let the stargazing begin ... skip 1 : 0 2 4 6 8 10 12 1 3 5 7 9 11 0 * skip 2 : 0 3 6 9 12 2 5 8 11 1 4 7 10 0 * skip 3 : 0 4 8 12 3 7 11 2 6 10 1 5 9 0 * skip 4 : 0 5 10 2 7 12 4 9 1 6 11 3 8 0 * skip 5 : 0 6 12 5 11 4 10 3 9 2 8 1 7 0 *
Drawing (by hand) the 4 unique 11-point stars, we get

It turns out that you will always get (p-3)/2 stars when p is prime!