This little known mathematical discipline has not, of recent years, received in the literature the attention which, in our opinion, it deserves.

In the present paper we present some algorithms which, it is hoped, may be of interest to other workers in the field. Neglecting the more obvious trivial methods, we shall confine our attention to those which involve significant applications of ideas familiar to mathematicians and physicists.

The present time is particularly fitting for the preparation of an account of the subject, since recent advances both in pure mathematics and in theoretical physics have made available powerful tools whose very existence was unsuspected by earlier investigators. At the same time, some of the more elegant classical methods acquire new significance in the light of modern discoveries. Like many other branches of knowledge to which mathematical techniques have been applied in recent years, the Mathematical Theory of Big Game Hunting has a singularly happy unifying effect on the most diverse branches of the exact sciences.

For the sake of simplicity of statement, we shall confine our attention to Lions (Felis leo) whose habitat is the Sahara Desert. The methods which we shall enumerate will easily be seen to be applicable, with obvious formal modifications, to other carnivores and to other portions of the globe. The paper is divided into three parts, which draw their material respectively from mathematics, theoretical physics, and experimental physics.

The author desires to acknowledge his indebtedness to the Trivial Club of St. John's College, Cambridge, England; to the M. I. T. chapter of the Society for Falicy Research; to the F. o. P., of Princeton University and to numberous (sic) individual contributors, known and unknown, conscious and unconscious.

1. Mathematical Methods

1. The Hilbert, or Axiomatic Method. We place a locked cage at a given point of the desert. We then introduce the following logical system.

Axiom I. The class of lions in the Sahara Desert is non-void.

Axiom II. If there is a lion in the Sahara Desert, there is a lion in the cage.

Rules of Procedure. If p is a theorem, and "p implies q" is a theorem, then q is a theorem.

Theorem I. There is a Lion in the cage.

2. The Method of Inversive Geometry. We place a spherical cage in the desert, enter it, and lock it. We perform an inversion with respect to the cage. The lion is then in the interior of the cage, and we are outside.

3. The Method of Projective Geometry. Without loss of generality, we may regard the Sahara Desert as a plane. Project the plane into a line, and the line into an interior point of the cage. The lion is projected into the same point.

4. The Bolzano-Weierstrass Method. Bisect the desert by a line running N-S. The lion is either in the E portion or in the W portion. Bisect this portion by a line running E-W. The lion is either in the N portion or in the S portion. We continue this process indefinitely, constructing a sufficiently strong fence about the chosen portion at each step. The diameter of the chosen portions approaches zero, so that the lion is ultimately surrounded by a fence of arbitrarily small perimeter.

5. The "Mengentheoretisch" Method. We observe that the desert is a separable space. It therefore contains an enumerable dense set of points, from which can be extracted a sequence having the lion as limit. We then approach the lion stealthily along this sequence, bearing with us suitable equipment.

6. The Peano Method. Construct, by standard methods, a continuous curve passing through every point of the dessert. It has been remarked (1) that it is possible to traverse such a curve in an arbitrarily short time. Armed with a spear, we traverse the curve in a time shorter than that in which a lion can move his own length.

7. A Topological Method. We observe that a lion has at least the connectivity of the torus. We transport the desert into four-space. It is then possible (2) to carry out such a deformation that the lion can be returned to three-space in a knotted condition. He is then helpless.

8. The Cauchy, or Functiontheoretical, Method. We consider an analytic lion-valued function f(z). Let ζ be the cage. Consider the integral:

1/(2*π*i)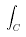

f(z)/(z - ζ) dz

where C is the boundary of the desert; its value is f(ζ), ie., a lion in the cage (3).

9. The Wiener Tauberian Method. We procure a tame lion, L₀, of class L(-∞,∞), whose Fourier transform nowhere vanishes, and release it in the desert. L then converges to our cage. By Wiener's General Tauberian Theorem, any other lion, L (say) will then converge to the same cage (4). Alternatively, we can approximate arbitrarily closely to L by translating L₀ about the desert (5).

2. Methods From Theoretical Physics

10. The Dirac Method. We observe that wild lions are, ipso facto, not observable in the Sahara Desert. Consequently, if there are any lions in the desert, they are tame. The capture of a tame lion may be left as an exercise for the reader.

11. The Schrodinger Method. At any given moment there is a positive probability that there is a lion in the cage. Sit down and wait.

12. The Method of Nuclear Physics. Place a tame lion in the cage, and apply a Major and exchange operator (6) between it and a wild lion. As a variant, let us suppose, to fix ideas, that we require a male lion. We place a tame lioness in the cage, and apply a Heisenberg exchange operator (7) which exchanges the spins.

13. A Relativistic Method. We distribute about the desert lion bait containing large portions of the Companion of Sirius. When enough bait has been taken, we project a beam of light across the desert. This will bend right around the lion, who will then become so dizzy that he can be approached with impunity.

3. Methods From Experimental Physics

14. The Thermodynamical Method. We construct a semi-permeable membrane, permeable to everything except lions, and sweep it across the desert.

15. The Atom-Splitting Method. We irradiate the desert with slow neutrons. The lion becomes radioactive, and a process of disintegration sets in. When the decay has proceded sufficiently far, he will become incapable of showing fight.

16. The Magneto-optical Method. We plant a large lanticular bed of catnip (Nepeta cataria), whose axis lies along the direction of the horizontal component of the earth's magnetic field, and place a cage at one of its foci. We distribute over the desert large quantities of magnetized spinach (Spinacia oleracia), which, as is well known, has a high ferric content. The spinach is eaten by the herbivorous denizens of the desert, which are in turn eaten by lions. The lions are then oriented parallel to the earth's magnetic field, and the resulting beam of lions is focussed by the catnip upon the cage.

---------------------------------------------------------------------

(1) By Hilbert. See E. W. Hobson. The Theory of Functions of a Real Variable and the Theory of Fourier's Series, 1927, vol. 1, pp. 456-7.

(2) H. Seifert and W. Threlfall, Lehrbuch der Topologie, 1934, pp. 2- 3.

(3) N.B. By Picard's Theorem (W.F. Osgood, Lehrbuch der Funktionentheorie, vol. 1, 1928, p. 748), we can catch every lion with at most one exception.

(4) N. Wiener, The Fourier Integral and Certain of its Applications, 1933, p. 73.

(5) N. Wiener, l.c., p. 89.

(6) See, for example, H. A. Beths and B. F. Bacher, Review of Modern Physics, vol. 8, 1936, pp. 82-225; especially pp. 106-7

(7) Ibid.