Our little language (TINY.EXE) might be strong enough to help kids understand elementary math concepts. Here's a problem that came up recently: What x values make
|1+5x|>=100
true, where the long vertical marks stand for absolute value? The above will be true if x is sufficiently large (positive) or if x is sufficiently large (negative). A program that lets x range from -30 to +30 and displays x when the above holds should do it.
`ABS.TIN - 10/3,4/2010 - lrb'
:""
x=-30
T y=1+5*x
{y>0}->P
y=-1*y
P {y<100}->B
;x
;" "
B x=x+1
{x<=30}->T
:""
!
C:\lee\tiny>TINY.EXE
tiny interpreter by Les Hancock - implemented by Lee Bradley (9/17/2010)
Name of program: ABS.TIN
-30 -29 -28 -27 -26 -25 -24 -23 -22 -21 20 21 22 23 24 25 26 27 28 29 30
C:\lee\tiny>
So, generalizing, it looks like the solution is (-∞,-21] ∪ [20,∞)
If x is allowed to be real (i.e. not just an integer) the exact solution can be seen to be
(-∞,-20 1/5] ∪ [19 4/5,∞)
and, with a little bit of work we could change the code to display something like
-20.2 and 19.8 for the mixed numbers.
`ABS.TIN - 10/3,4,5/2010 - lrb'
:""
x=-22
T y=33+5*x
{y>0}->P
y=-1*y
P :""
{x>=0};" "
;x
;" "
k=y/3
{x<10}{x>=0};" "
{x>-10}{x<0};" "
H {k<0}->B
;"."
k=k-1
->H
B ;" "
;y
x=x+1
{x<=22}->T
:""
!
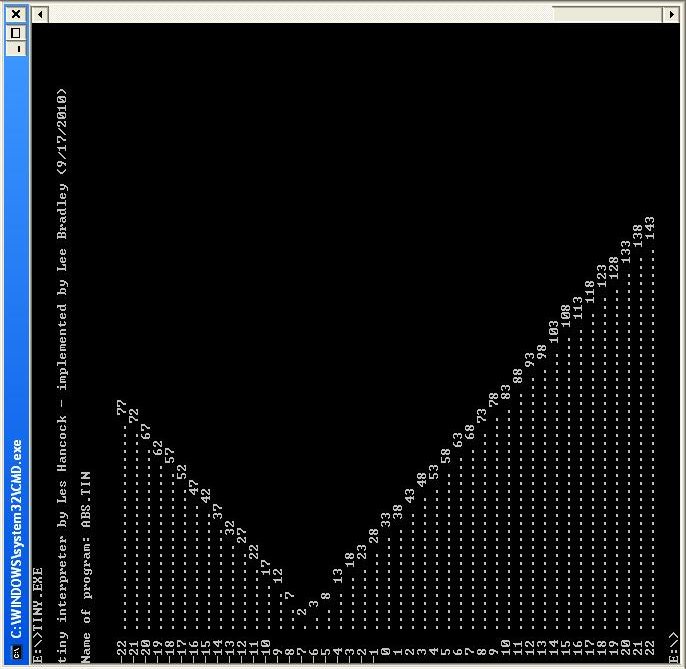
Discussion:
The function is now y=|33+5x| and we've altered the program to plot the values. (The output has been rotated 90° counterclockwise so the x- and y-axes are in their standard place.) The x values that cause y to be greater than (less than), say, 38, are easily spotted. They are x>1 or x<-14 (-14<x<1). These results can be determined analytically (and more precisely) to be x>1 or x<-14 1/5 (-14 1/5<x<1)
Notice how we use two if statements in a row ({ }{ }) to implement a logical and. This was done to add a space after the single-digit x values.