A Sequence Problem

Lee Bradley
March 16, 2012

Consider the sequence (0, 3, 18, 69, 228, 711...) Find a recursive equation for the terms and a closed form solution for the nth term.

It's interesting to try to figure out what the patterns are in such things. I saw that the numbers were all divisible by 3 and that each term was, roughly, 3 times the term that preceded it. So, to begin, I wrote things like

18 = 3(3) + 9
69 = 3(18) + 15
228 = 3(69) + 21

Then I saw that the number I had to add was itself divisible by 3.

18 = 3(3) + 3(3)
69 = 3(18) + 3(5)
228 = 3(69) + 3(7)

Then I "saw it!"

The recursive equation x_n+1 = 3(x_n) + 3(2n - 1) with x₁ = 0 can be seen to generate the sequence.

This equation can also be written x_n+1 - 3(x_n) = 3(2n - 1).

This is an example of an inhomogeneous difference equation. Techniques for solving such equations parallel those for solving inhomogeneous differential equations.

Let's see if a particular solution which has the form p_n = A + Bn can be found.

p_n+1 = A + B(n+1) = 3(A + Bn) + 6n - 3

A + Bn + B = 3A + 3Bn + 6n - 3

Equating constant and variable terms

A + B = 3A - 3    B = 3B + 6

And solving

B = -3    A = 0

So p_n = -3n.

It can be proved that if p_n is a particular solution to the equation x_n+1 = ax_n + b_n where b_n is a function of n then caⁿ + p_n is also a solution.

In our case, a = 3. We evaluate c from the condition x₁ = 0.

c3 - 3 = 0 which implies c = 1.

A closed form solution is thus x_n = 3ⁿ - 3n.

The first few terms of the sequence are

The above is generated using JavaScript. JavaScript can't handle integers larger than about 3³². If you want to see the 999th and the 99999th terms, visit http://primepuzzle.com/tunxis/large-numbers.html!

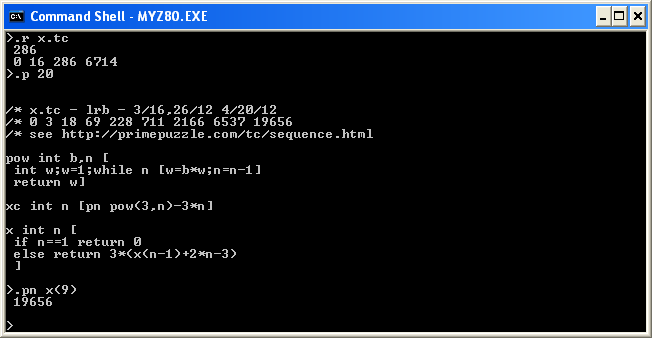
A screenshot of x.tc which computes this sequence using both the recursive and closed form methods follows. This is a program in tiny-c, a C-like language.