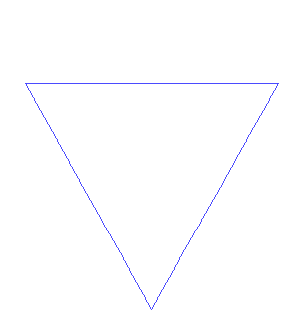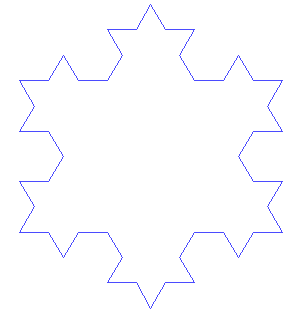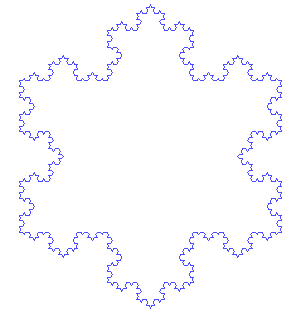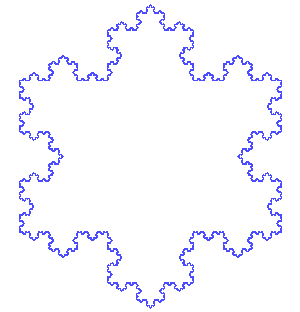
The area of an equilateral triangle with side a is (√3/4)a^2. The area enclosed by a Koch snowflake is 8/5 times the area of the generating equilateral triangle. A = (√3/4)(1 + 3(1/3)^2 + (4)(3)(1/3^2)^2 + (4)(4)(3)(1/3^3)^2 + ...) = (√3/4)(1 + 1/3 + 12/9[1/9 + (1/9)(4/9) + (1/9)(4/9)^2 + ...]) = (√3/4)(1 + 1/3 + (4/3)(1/9)[1 + 4/9 + (4/9)^2 + ...]) = (√3/4)(4/3 + (4/3)(1/9)(1/(1 - 4/9))) = (√3/4)(4/3)(1 + (1/9)(9/5)) = (√3/4)(4/3)(6/5) = (√3/4)(8/5)