Rick -

This post (http://www.exploringbinary.com/powers-of-two-in-the-josephus-problem/ ) reminds me of something that I worked on some time back. There are many more differences than similarities between your problem and mine but you may find this interesting.

The problem involved the following question: How many different n-point stars can you draw?

The construction rule for the way to draw a 5-point star goes like this:

Start at point A and draw a line to point C. Then draw a line from C to E. Then from E to B. Then from B to D. Then from D back to A.

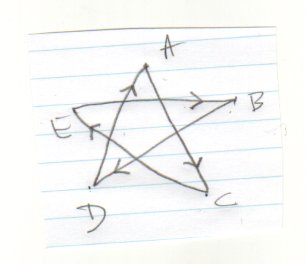
One way to describe this method would be to say "skip 1 letter" each time. If we label the points with numbers we see that the following sequence describes the drawing route.

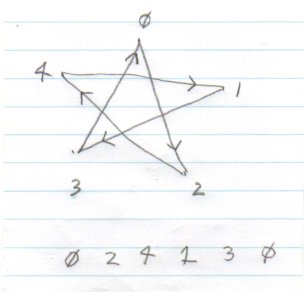
If you try "skip 2" you will see that what you get is not really different but is just the first star, drawn backwards.

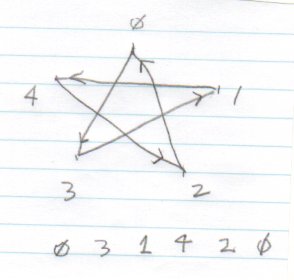
If you try "skip 3" or "skip 4" you get what I call "degenerate" cases.

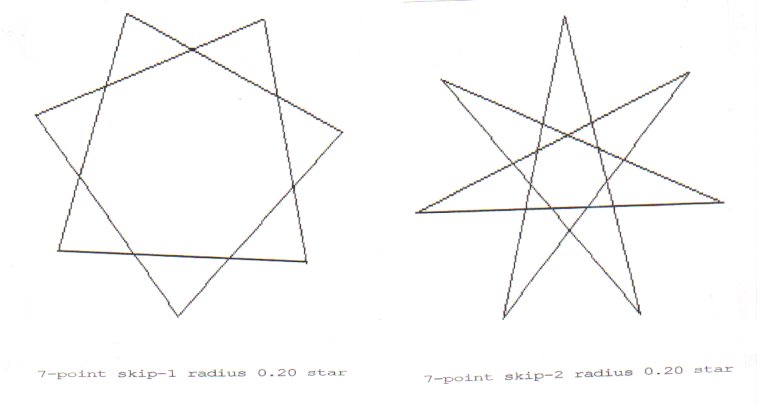
Try this approach on a 7-point star. Then on an 8-point star. Be very careful when you draw and record your findings.

Drawing (by hand) the 4 unique 11-point stars, we get

Generated number sequences that contain the number p-1, where p is the number of points, correspond to successfully drawn stars.

Once I realized this fact, I wrote a computer program to do the work for me. You quickly realize you need to do this after trying to draw the stars with 10 or more points!

Here are the two 7-point stars.

Here are the 7 different stars you get when there are 17 points.

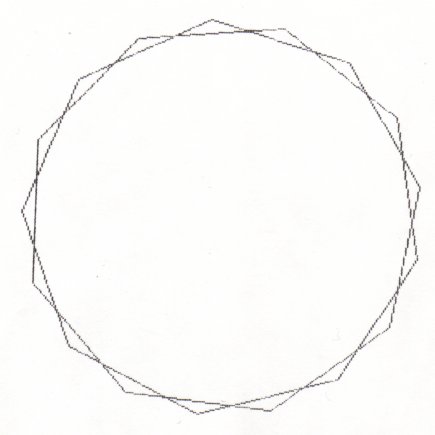
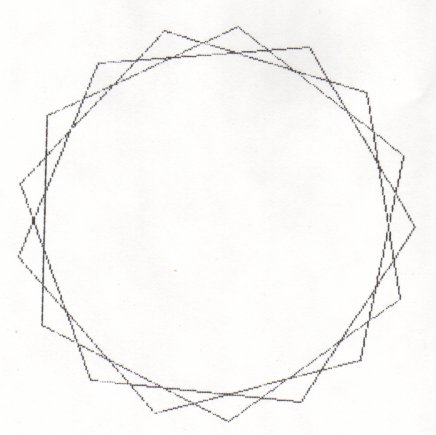
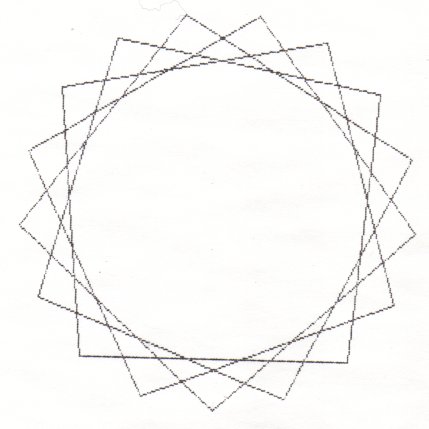
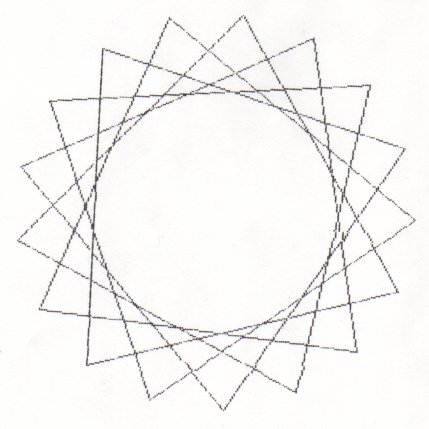
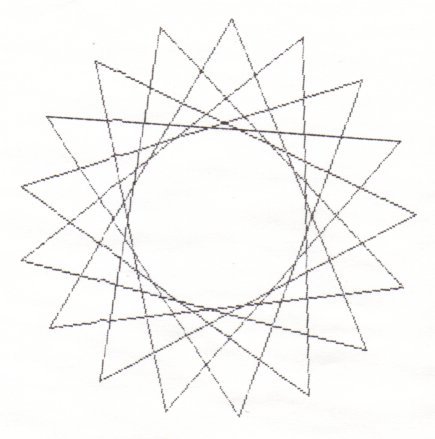
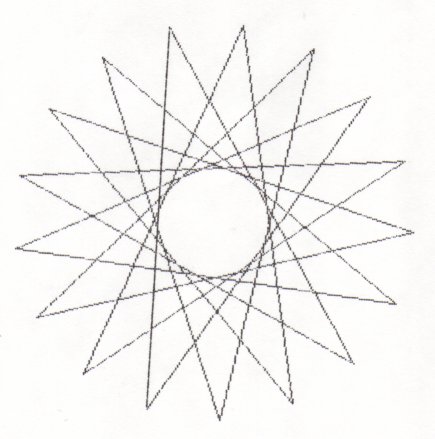
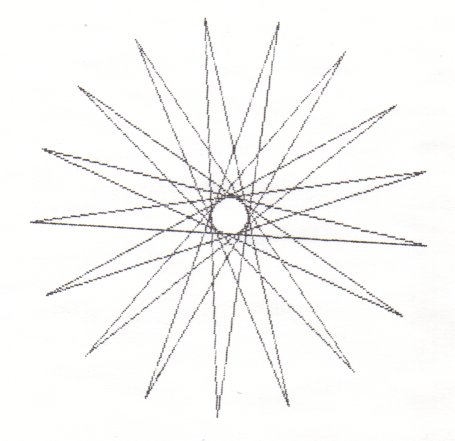
If p is prime you will always get (p-3)/2 stars!

The number of unique n-point stars that can be drawn, where n is any number, composite or prime, is related to phi(n), the "totient" of n.

The "totient" of n is the number of numbers that are "coprimes" of n. This means they have no common factors with n. The number 60 has the following coprimes:

1 7 11 13 17 19 23 29 31 37 41 43 47 49 53 59

It can be shown that

phi(n) = n * (p1-1)/p1 * (p2-1)/p2 ...

where the p's range over the unique prime factors of n.

The number of n-point stars = (phi(n)-2)/2

Since 60 = 2 * 2 * 3 * 5, we have

phi(60) = 60 * 1/2 * 2/3 * 4/5 = 16

The number of unique 60-point stars = (16-2)/2 = 7

Note: If n is prime, the above formula reduces to the (p-3)/2 formula above because

phi(p) = p * (p-1)/p = p-1

so

(phi(p)-2)/2 = (p-1-2)/2 = (p-3)/2

"Extra Credit Quiz"

How many 1000-point stars are there?

- Lee