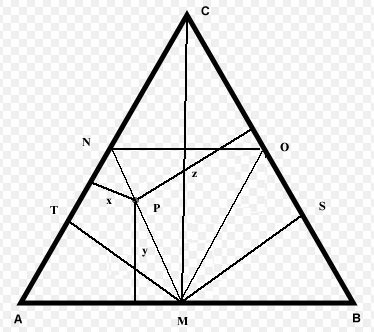
Points M, N and O are the midpoints of the sides of equilateral triangle ABC. Altitude CM = 1.

Viviani's theorem states that the sum of the distances from a point P to the sides of an equilateral triangle equals the length of the triangle's altitude (and is thus independent of where the point P is placed). From this we see

x + y + z = 1 (Eq. 1)

For the lines of length x, y and z to form a triangle, assuming z is the longest, it must be that

x + y > z (Ineq. 1)

If we let P travel along the line MN, it's clear that z is constant. When P is at M, y = 0. So x + 0 + z = 1 (by Eq. 1). But x = z here (right triangles ATM and MSB are congruent). So 2*z = 1 or z = 1/2. Clearly, all z's for P inside triangle AMN are > 1/2. This implies x + y < 1/2 (by Eq. 1). This implies Ineq. 1 doesn't hold. So no P in triangle AMN will have x, y and z that will form a triangle.

For P's in the other two "outer" triangles, just rotate the figure 120 degrees (counter)clockwise to show P's in them can't make triangles. For P's in the interior triangle, z < 1/2 and thus x + y must be > z, so triangles can be formed.

Since the area of the interior triangle NMO is 1/4 the area of the whole triangle ABC, we see that the probability of getting three pieces that form a triangle is 1/4.